قواعد علامتگذاری گشتاورهای خمشی
یکی از نکات اصلی در تحلیل گشتاورهای خمشی، تعیین قواعد علامتگذاری پیش از شروع تحلیل است. به این منظور، با ایجاد یک برش درون تیر، وضعیت بارهای اعمال شده بر سطح مقطع آن را مطابق شکل زیر مورد بررسی قرار میدهیم. در شکل زیر از بردارهای دو پیکانی برای نمایش گشتاور خمشی My حول محور y و گشتاور خمشی Mz حول محور z استفاده شده است.
اگر نوک پیکان بردار گشتاور به سمت مثبت محور مربوطه اشاره کند، علامت آن مثبت خواهد بود. جهت چرخش گشتاور با استفاده از قانون دست راست بردارها به دست میآید (با قرار دادن انگشت شست در راستای اعمال بردار و تعیین ساعتگرد/پادساعتگرد بودن جهت چرخش با بررسی جهت چرخش باقی انگشتها).
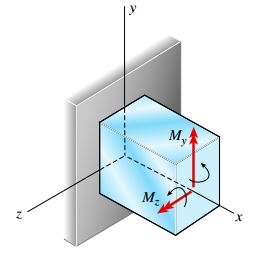
با توجه به شکل بالا، گشتاور خمشی مثبت My باعث ایجاد فشار در بخش سمت راست تیر (بخش منفی محور z) و کشش در بخش سمت چپ آن (بخش مثبت محور z) میشود. به همین ترتیب، گشتاور خمشی مثبت Mz، بخش بالایی تیر (بخش مثبت محور y) را تحت فشار و بخش پایینی آن (بخش منفی محور y) را تحت کشش قرار میدهد. علاوه بر این، توجه داشته باشید که گشتاورهای خمشی نمایش داده شده در شکل بالا، بر روی بخش مثبت محور x اعمال میشوند. در نتیجه، این گشتاورها بر وی صفحهای قرار دارند که بردار نرمالش به جهت مثبت محور x اشاره میکند.
تنشهای نرمال (تنشهای خمشی)
تنشهای نرمال حاصل از اعمال گشتاورهای خمشی My و Mz توسط رابطه پیچش مورد ارزیابی قرار میگیرند. پس از تعیین این تنشها، تنشهای ناشی از اعمال همزمان گشتاورها با استفاده از برهمنهی تنشهای نرمال محاسبه میشوند. به عنوان مثال، تنشهای موجود در یکی از نقاط موجود بر روی مقطع عرضی زیر (نقطه A) را در نظر بگیرید. این نقطه در بخش مثبت محورهای y و z قرار دارد.

اعمال گشتاور مثبت My باعث ایجاد کشش در نقطه A و اعمال گشتاور مثبت Mz منجر به ایجاد کشش در نقطه مذکور میشود. به این ترتیب، تنش نرمال در نقطه A برابر است با:

Iy و Iz به ترتیب ممان اینرسی سطح مقطع تیر نسبت به محورهای y و z را نمایش میدهند. با استفاده از رابطه بالا میتوان تنشهای نرمال موجود در هر نقطه دلخواه بر روی سطح مقطع را محاسبه کرد. به این منظور، تنها باید مقادیر جبری گشتاورها و مختصات آنها را درون این رابطه قرار داد.
محور خنثی
اگر تنش نرمال σx را برابر با صفر قرار دهیم، معادله مورد نیاز برای تعیین مختصات محور خنثی به دست میآید:

این معادله نشان میدهد که محور خنثی nn به صورت یک خط راست گذرنده از مرکز هندسی C است.

زاویه بین محور خنثی و محور z از طریق رابطه زیر محاسبه میشود:

زاویه β بین مقادیر °90- تا °90+ تغییر میکند. مقدار و علامت به دست آمده برای این زاویه به مقدار و جهتگیری گشتاورهای خمشی بستگی دارد.
اطلاع از نحوه جهتگیری محور خنثی برای تعیین محل رخ دادن تنش نرمال ماکسیمم بر روی مقطع عرضی به کار میآید. به دلیل رابطه خطی بین مقدار تنش و فاصله آنها تا محور خنثی، تنش ماکسیمم در دورترین نقطه (بیشترین فاصله) از محور خنثی رخ میدهد.تیرهای دارای تقارن
رابطه بین محور خنثی و زاویه اعمال بار
همانطور که در بخش قبلی نیز اشاره شد، جهتگیری محور خنثی نسبت به محور z با استفاده از گشتاورهای خمشی و ممانهای اینرسی مشخص میشود. مرحله بعدی، تعیین جهتگیری محور خنثی نسبت به زاویه اعمال بار بر روی تیر است. به این منظور، تیر یکسر گیردار زیر را در نظر بگیرید. این تیر در معرض نیروی P قرار دارد که بر روی آخرین مقطع عرضی تیر اعمال میشود. زاویه بین نیروی مذکور با جهت مثبت محور y برابر با θ است. در این جهتگیری بخصوص، گشتاورهای خمشی Myو Mzدر محدوده θ=0 تا °θ=90 دارای علامت مثبت هستند.

به منظور تسهیل فرآیند تحلیل میتوانیم بار P را به دو مؤلفه Pcosθ در جهت مثبت محور y و Psinθ در جهت منفی محور z تجزیه کنیم. به این ترتیب، گشتاورهای خمشی اعمال شده بر سطح مقطع (Myو Mz) در فاصله x از تکیهگاه ثابت تیر از روابط زیر به دست میآیند:
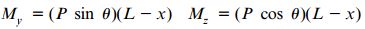
L: طول تیر
نسبت این دو گشتاور برابر است با:
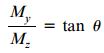
نسبت بالا نشان میدهد که بردار برآیند گشتاور M در زاویه θ نسبت به محور z قرار دارد. در نتیجه، بردار برآیند گشتاور به صفحه طولی دربرگیرنده نیروی P عمود است. مقدار زاویه β در فاصله بین محور خنثی nn و محور z نیز به صورت زیر تعیین میشود:

طبق رابطه بالا، زاویه β معمولاً با زاویه θ برابر نیست. بنابراین، محور خنثی در اغلب موارد بر صفحه طولی دربرگیرنده بار اعمال شده عمود نخواهد بود؛ مگر اینکه یکی از حالتهای خاص زیر در مسئله وجود داشته باشد:
- زمانی که بار بر روی صفحه xy (زاویه θ=0 یا θ=180) قرار داشته باشد. در این حالت، محور z همان محور خنثی است.
- زمانی که بار بر روی صفحه xz (زاویه θ=±90) قرار داشته باشد. در این حالت، محور y همان محور خنثی است.
- زمانی که ممانهای اینرسی با هم برابر باشند (Iy=Iz).
در حالت سوم از موارد بالا، تمام محورهای گذرنده از مرکز هندسی سطح مقطع به عنوان محورهای اصلی در نظر گرفته میشوند؛ چراکه مقدار ممان اینرسی تمامی آنها با یکدیگر برابر است.صفحه اعمال بار نیز همیشه به عنوان یکی از صفحات اصلی بوده و بر محور خنثی عمود است. این حالت در تیرهایی با سطح مقطع دایرهای و مربعی رخ میدهد.تیرهای دارای تقارن
به این ترتیب در حالت کلی، هیچ الزامی به عمود بودن محور خنثی بر صفحه اعمال بار وجود ندارد. این نکته، تأثیر زیادی بر روی تنشهای موجود در تیر میگذارد؛ مخصوصاً اگر نسبت ممانهای اینرسی اصلی عدد بزرگی باشد. در این شرایط، حساسیت تنشهای موجود در تیر به تغییر جهت اعمال بار و همچنین تغییر راستای تیر افزایش مییابد. در مثالهای انتهای مقاله میتوان این ویژگی را به خوبی مشاهده کرد.